Entropy Changes in Mixing Ideal Gases

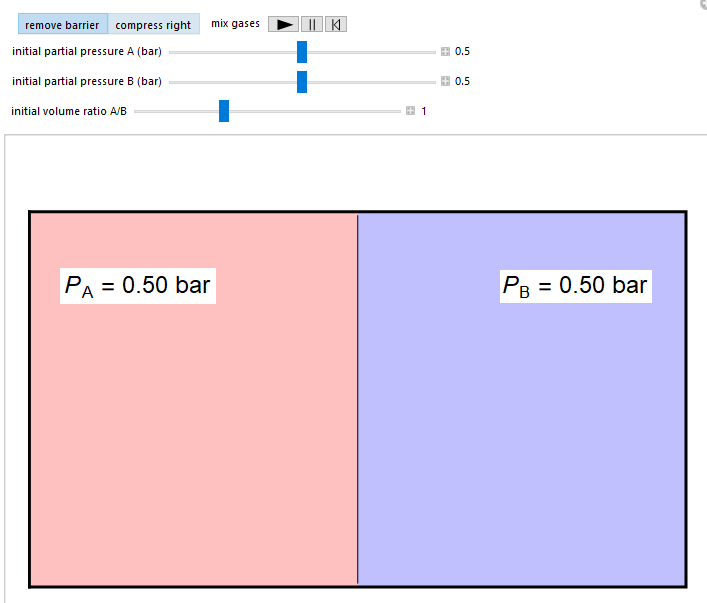
In this simulation, ideal gases A and B are mixed isothermally by keeping the total volume constant (“remove barrier” option) or by adding gas A to gas B so the final volume is the same as the initial volume of B (“compress right” option). Select the “mix gases” play button to initiate mixing. For the “remove barrier” option, the entropy change of each gas is the same as that of a gas expanding into a vacuum. When the partial pressure decreases, entropy increases. For the “compress right” option, if the partial pressure of a gas does not change, its entropy does not change, even when mixed with another gas. The total entropy change is the sum of the entropy changes of each gas. Gas A is colored red and gas B is colored blue, and when the gases mix, different shades of purple result, depending on the ratio of moles of each species. As the number of moles increases, the color becomes more intense. When the initial pressures of A and B are equal and the “remove barrier” option is selected, which corresponds to mixing at constant pressure, the entropy of mixing is: \[ \Delta S_{mix} = -n_{A} \mathrm{ R } \; \mathrm{ln}(x_{A}) – n_{B} \mathrm{ R } \; \mathrm{ln}(x_{B}) \] where \( x_{A} \) and \( x_{B} \) are the mole fractions of A and B in the final mixture.
This simulation runs on desktop using the free Wolfram Player. Download the Wolfram Player here.
About:
This simulation was made at the University of Colorado Boulder, Department of Chemical and Biological Engineering. Author: Derek M. Machalek
View the source code for this simulation
