Diffusion and Reaction in a Catalyst Pellet

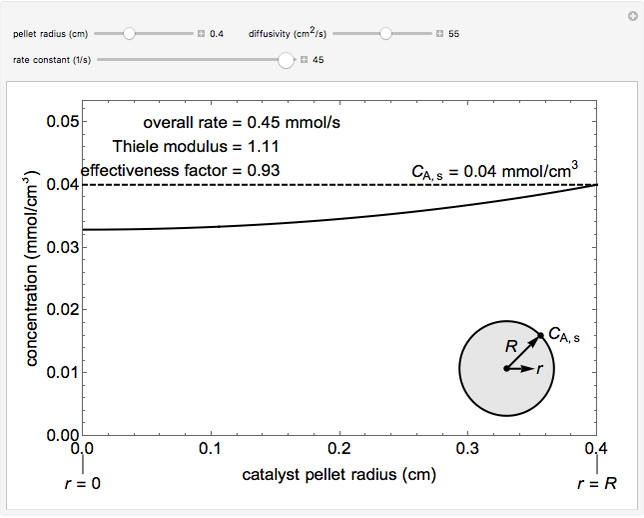
The overall rate of reaction in an isothermal, porous, spherical catalyst pellet is calculated for a first-order, gas-phase reaction that is limited by diffusion in the catalyst pores. This simulation plots the reactant concentration inside the catalyst pellet versus the pellet radius. Use the sliders to set the pellet radius, diffusivity and reaction rate constant. The Thiele modulus is a dimensionless number that represents the ratio of reaction rate to diffusion rate. The effectiveness factor is the overall rate of reaction divided by the rate of reaction if the entire catalyst were at CA,s = 0.04 mmol/cm3 (the external surface concentration). The diffusivity slider represents diffusivity DAB, not effective diffusivity De. The value used for pellet porosity f is 0.4, constriction factor s is 0.8, and tortuosity t is 3.
This simulation runs on desktop using the free Wolfram Player. Download the Wolfram Player here.
About:
This simulation was made at the University of Colorado Boulder, Department of Chemical and Biological Engineering. Author(s): Rachael L. Baumann, John L. Falconer
View the source code for this simulation
