Heating Water and Air in a Sealed Container

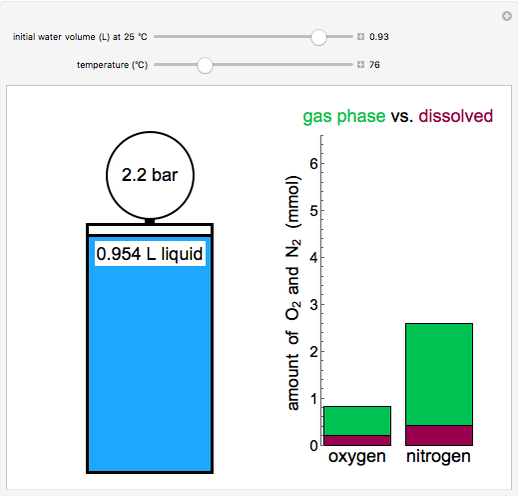
This simulation models the behavior of a sealed, 1-L autoclave that initially contains mostly water plus a small volume of air, all at 25°C. The initial volume of water is changed with a slider, and the temperature resets to 25°C when the initial water volume is changed. As the temperature increases by moving the slider, liquid water expands and its saturation pressure increases. At the same time, the gas-phase volume decreases, so gas-phase O2 and N2 partial pressures increase (ideal gas law). The amounts of O2 and N2 dissolved in the water increase with pressure, but decrease with temperature. The amounts dissolved are shown in the bar chart (green = gas phase, purple = dissolved). Even at moderate temperatures, the pressures inside the sealed container can be quite high.
This simulation runs on desktop using the free Wolfram Player. Download the Wolfram Player here.
About:
This simulation was made at the University of Colorado Boulder, Department of Chemical and Biological Engineering. Authors: Derek M. Machalek, Rachael L. Baumann
View the source code for this simulation
