Chemical Equilibrium in the Haber Process

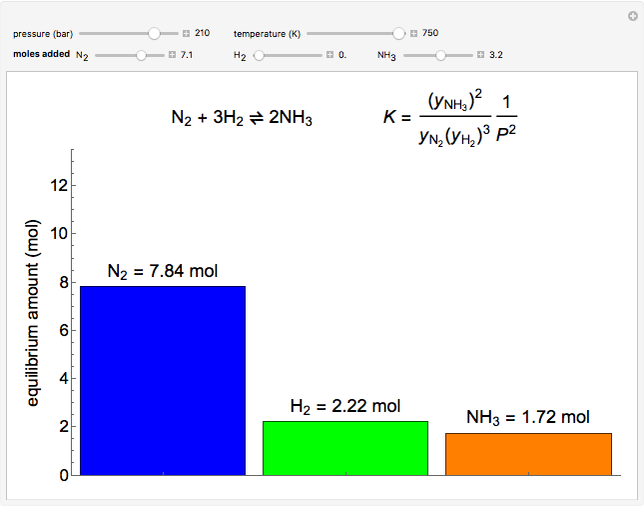
The number of moles at equilibrium is calculated for the Haber process, the reversible, exothermic reaction that synthesizes ammonia (NH3) from hydrogen (H2) and nitrogen (N2). The reaction is typically carried out at around 200 bar and 675–725 K. Sliders vary the pressure and temperature. Gases are assumed to behave ideally, although at the high pressures used for this reaction, the gases are nonideal. Four moles of reactants form two moles of product, so raising the pressure shifts equilibrium toward products. Initially, the system is filled with one mole of NH3 and allowed to reach equilibrium. Additional N2, H2, and/or NH3 at can be added at constant pressure, and the effect on the equilibrium is observed. Le Chatelier’s principle predicts that when N2 or H2 are added, the reaction goes to the right, whereas when NH3 is added, the reaction shifts to the left. However, when the N2/H2 ratio is sufficiently high, adding N2 shifts reaction to the left (i.e., adding N2 decreases the amount of NH3 and increases the amount of H2), contrary to what Le Chatelier’s principle predicts. This happens because adding N2 decreases the mole fraction of H2, and because the H2 mole fraction is cubed in the equilibrium expression, NH3 reacts to increase the number of moles of H2 and N2.
This simulation runs on desktop using the free Wolfram Player. Download the Wolfram Player here.
About:
This simulation was made at the University of Colorado Boulder, Department of Chemical and Biological Engineering. Authors: Benjamin L. Kee, Rachael L. Baumann
View the source code for this simulation
Chemical Equilibrium in the Haber Process


Description
The number of moles at equilibrium is calculated for the Haber process, the reversible, exothermic reaction that synthesizes ammonia (NH3) from hydrogen (H2) and nitrogen (N2). The reaction is typically carried out at around 200 bar and 675–725 K. Sliders vary the pressure and temperature. Gases are assumed to behave ideally, although at the high pressures used for this reaction, the gases are nonideal. Four moles of reactants form two moles of product, so raising the pressure shifts equilibrium toward products. Initially, the system is filled with one mole of NH3 and allowed to reach equilibrium. Additional N2, H2, and/or NH3 at can be added at constant pressure, and the effect on the equilibrium is observed. Le Chatelier’s principle predicts that when N2 or H2 are added, the reaction goes to the right, whereas when NH3 is added, the reaction shifts to the left. However, when the N2/H2 ratio is sufficiently high, adding N2 shifts reaction to the left (i.e. adding N2 decreases the amount of NH3 and increases the amount of H2), contrary to what Le Chatelier’s principle predicts. This happens because adding N2 decreases the mole fraction of H2, and because the H2 mole fraction is cubed in the equilibrium expression, Nh3 reacts to increase the number of moles of H2 and N2.
