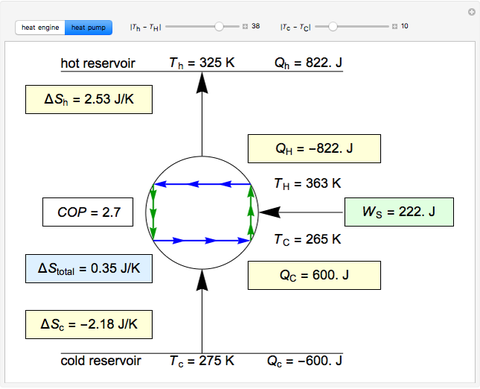
This simulation shows Carnot cycles operating both as a heat engine and as a heat pump, with finite temperature differences between the hot and cold reservoirs and the high and low temperatures parts of the Carnot cycle, respectively. The entropy changes for the reservoirs, \( \Delta S_{h} \) and \( \Delta S_{c} \), are calculated, as is the overall entropy change \( \Delta S_{total} \). When the temperature differences between the reservoir and the engine/pump are nonzero, the total entropy change is positive. The entropy change of the engine/pump, which is at steady state, is zero. All energies and entropy changes are expressed per unit time, since these are continuous processes, but the time scale is arbitrary. The cycle efficiency \( \eta \) is calculated for the heat engine, and the coefficient of performance (COP) is calculated for the heat pump. As the temperature difference between the reservoirs and the engine/pump increases, the efficiency or the coefficient of performance decreases. For the Carnot heat engine, the value of \( Q_{H} \) is held constant as the temperature differences change. For the heat pump, the value of \( Q_{C} \) is held constant as the temperature differences change. For the heat engine, the reservoir temperatures are held constant at 275 K and 500 K. For the heat pump, the reservoir temperatures are held constant at 275 K and 325 K.

Download this simulation

This simulation runs on desktop using the free Wolfram Player. Download the Wolfram Player here.

About:

This simulation was made at the University of Colorado Boulder, Department of Chemical and Biological Engineering.  Author(s): Rachael L. Baumann

---

View the source code for this simulation