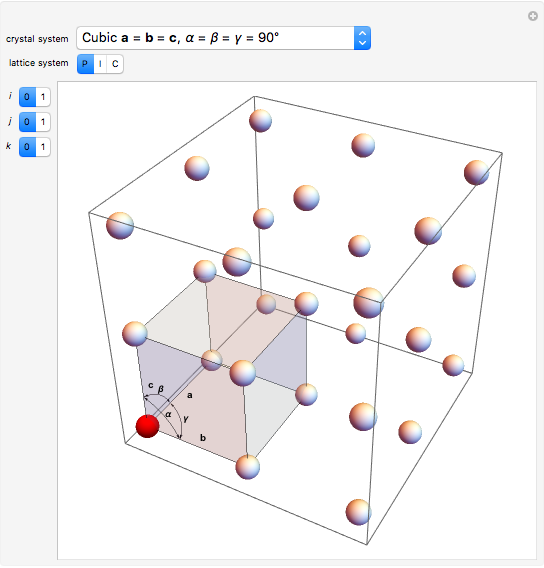
This simulation shows the characteristics of 3D Bravais lattices arranged according to seven crystal systems: cubic, tetragonal, orthorhombic, monoclinic, triclinic, rhombohedral and hexagonal. Each crystal system can be further associated with between one and four lattices by adding to the primitive cell (click “P”): a point in the center of the cell volume (click “I”), a point at the center of each face (click “F”) or a point just at the center of the base faces (click “C”). The points located at the center/faces are highlighted in blue; each point is also a vertex or center of the cell/face, therefore each point is equivalent to every other point.