Scale-Up of a Batch Reactor
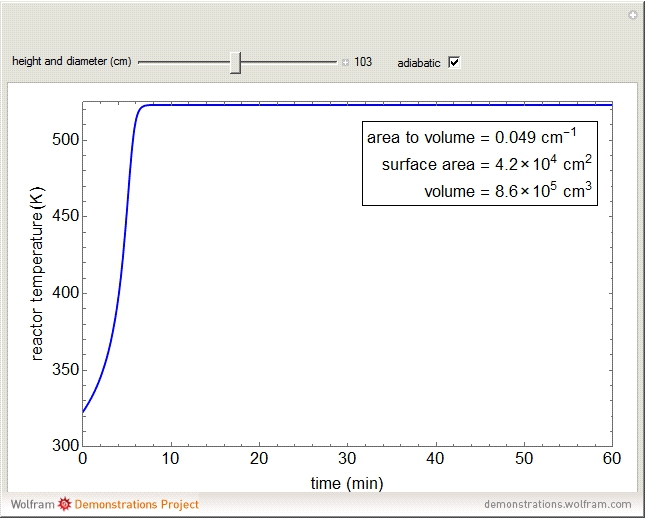
This simulation shows why a batch reactor with a cooling jacket cannot be scaled up geometrically. That is, as the diameter and height of the reactor increases, the surface area for heat transfer divided by the volume decreases, and thus the maximum temperature increases. This example is for an exothermic, liquid-phase, first-order reaction. The diameter and height of the reactor are equal. A cooling jacket around the outside of the reactor transfers heat away from the reactor. As the reactor size increases, the maximum temperature approaches the adiabatic limit. Adiabatic reactor behavior is shown by selecting the adiabatic checkbox. This is independent of the reactor size.
This simulation runs on desktop using the free Wolfram Player. Download the Wolfram Player here.
About:
This simulation was made at the University of Colorado Boulder, Department of Chemical and Biological Engineering. Author: Rachael L. Baumann
View the source code for this simulation