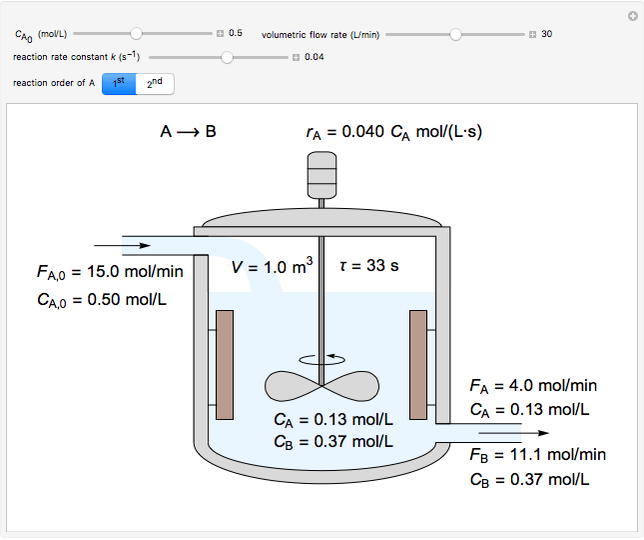
In this simulation, the liquid-phase reaction (A –> B) takes place in an isothermal, continuous stirred-tank reactor (CSTR). Use the sliders to set the feed concentration of A, (C_A,0), the volumetric flow rate (v) and the rate constant (k). Select the reaction order with respect to A using the (1^st) or (2^nd) button. The rate constant has the same numerical value when the reaction order changes, but its units are different. The figure shows the feed molar flow rate (F_A,0), the feed concentration (C_A,0), the outlet molar flow rates (F_A, F_B) and the outlet concentrations (C_A, C_B). Note that the outlet concentrations are identical to the concentrations in the reactor. The reactor residence time (t = V/v) is also calculated.

Download this simulation

This simulation runs on desktop using the free Wolfram Player. Download the Wolfram Player here.

About:

This simulation was made at the University of Colorado Boulder, Department of Chemical and Biological Engineering.  Author(s): Neil Hendren

---

View the source code for this simulation