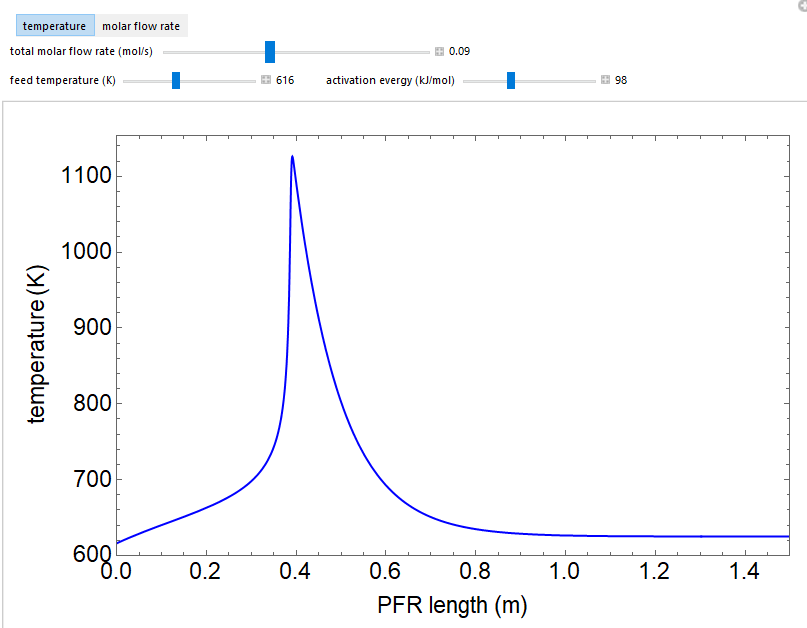
This simulation plots the temperature and molar flow rate of the reactant as a function of distance down a plug flow reactor for an exothermic, gas-phase reaction. The reactor has heat exchange through the walls. Vary the feed temperature, activation energy for the reaction, and total molar flow rate with the sliders. Thermal runaway occurs at certain conditions and it is a sensitive function (parametric sensitivity) of the feed temperature and the activation energy.

Download this simulation

This simulation runs on desktop using the free Wolfram Player. Download the Wolfram Player here.

About:

This simulation was made at the University of Colorado Boulder, Department of Chemical and Biological Engineering.  Author: Rachael L. Baumann

View the source code for this simulation