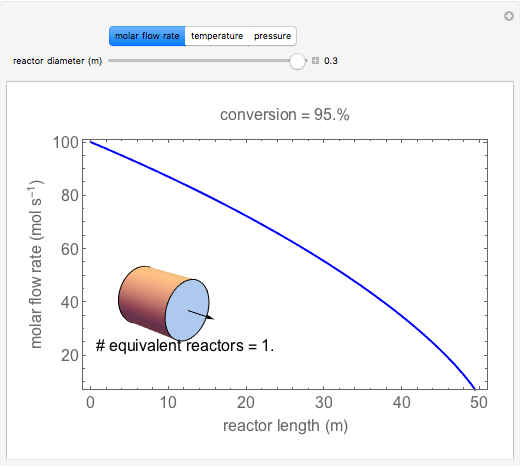
A first-order, exothermic reaction takes place in a plug flow reactor (PFR) that has pressure drop and heat transfer through the walls. Use the slider to observe the effects of changing reactor diameter; the total feed flow rate is kept constant by changing the number of parallel reactors (number of equivalent reactors) so that the total reactor cross section does not change. Use buttons to observe how reactant molar flow rate, temperature, and pressure depend on reactor length. For small-diameter reactors, the pressure drop is higher, which increases the volumetric flow rate and reduces the residence time; this lowers conversion. Since heat transfer is more efficient for smaller-diameter reactors because the surface area per volume is larger, the temperature increases less; this also lowers conversion.

Download this simulation

This simulation runs on desktop using the free Wolfram Player. Download the Wolfram Player here.

About:

This simulation was made at the University of Colorado Boulder, Department of Chemical and Biological Engineering.  Author: Rachael L. Baumann

View the source code for this simulation