Double-Sided Couette Flow

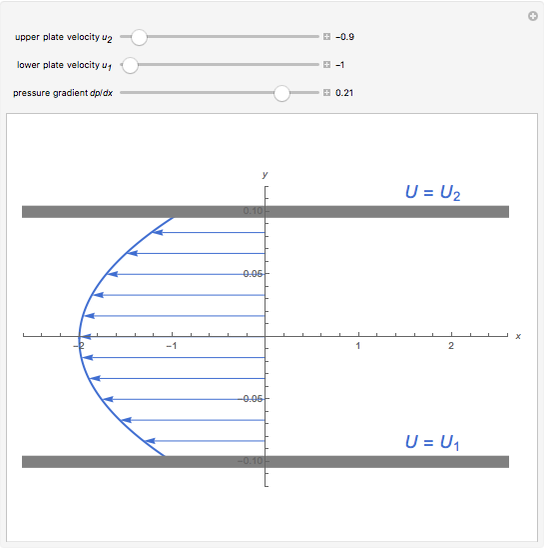
Description
The laminar flow of an incompressible viscous fluid in the space between two parallel plates can be described by a linear ODE for u(y): d2u/dy2 = 1/m dp/dx where m is the dynamic viscosity of the fluid and dp/dx is the pressure gradient. The boundary conditions are u(-h) = u1 (lower plate velocity) and u(h) = u2 (upper plate velocity)
This simulation runs on desktop using the free Wolfram Player. Download the Wolfram Player here.
About
Authors: David Gerhardinger, William C. Guttner. Open content licensed under CC BY-NC-SA.
View the source code for this simulation
